2. 机器学习基础¶

机器学习是人工智能的核心技术，经过多年的发展，已经成为一门多领域交叉的学科，涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等，并广泛应用于计算机视觉、自然语言处理、语音识别、数据挖掘、生物特征识别、搜索引擎、医学诊断、DNA序列测序和机器人控制等领域。本章将从基本概念、学习范式、损失与优化三个方面概念性的介绍机器学习的基础知识，以便读者更好的了解机器学习的核心要素和基本流程。只有充分的了解机器学习才能更好的揭示其所存在的安全问题以及问题的根源，从而可以启发更高效的解决方案。

2.1. 基本概念¶

机器学习通常指模型从有限的训练样本中利用学习算法自动寻找规律和知识，进而在未知数据上进行决策的过程。在机器学习过程中，我们需要根据特定的学习任务设计数学模型，确定从输入到输出的具体映射形式，然后再定义目标函数衡量拟合程度，设计优化策略在训练集上对模型进行迭代更新直到达到目标函数最优值。我们在验证集上检验模型的泛化能力并挑选最优的模型参数，并最终在测试集上进行模型评估。为了更好地理解机器学习的概念，本小节将从学习任务、知识来源、学习主体、学习算法以及学习目标等方面一一进行阐述。

机器学习任务是指人为定义的一种方便机器完成的最简问题。一个具体的机器学习任务往往源自一个现实世界的问题，具有明确定义的“输入”和“输出”，并且可以通过一定的手段采集到样例“输入”和“输出”。机器学习任务形式多样，比如在棋类游戏中根据当前的棋盘局势落子、识别图片中物体的种类、讲一段中文翻译成英文等。现实世界中的问题，简单或复杂，都可以分解成一个或者多个机器学习任务。是否可拆分的关键是中间步骤的产物是否可捕获或者可观测。机器学习概念始于1959年，经过多年的发展已经研究了大量的学习任务，其中主要的任务类型包括回归、分类、生成、降噪、异常检测、机器翻译等。

当学习任务得到明确定义以后，我们就可以在应用场景中收集输输入输出样本，以构建训练数据集。在数据收集过程中最重要的一个假设是数据独立同分布（independent and identically distributed, IID）假设，即每一个样本（训练样本和测试样本）都是从同一个分布（形式未知）随机独立采样得到的。独立同分布假设保证了机器学习模型在训练样本上训练后可以在未知（测试）样本上进行泛化，是机器学习模型泛化的关键，而实际上，很多泛化问题的出现都跟打破独立同分布假设有关。因此在收集训练样本时，往往要求多次采样之间应尽可能的独立，且希望采样出来的数据点都服从同一分布。单一数据样本可由一个多维度向量表示如下：

(2.1.1)¶\[{x}_i= ({x}_i^{(1)}, {x}_i^{(2)}, \ldots, {x}_i^{(d)})^{\top}.\]

多个训练样本组成一个训练样本集（不包含标签），我们用$X$表示训练样本集，定义如下：

(2.1.2)¶\[X = \{{x}_1, {x}_2, \ldots, {x}_n\}.\]

机器学习的对象是数据中蕴涵的知识。 机器学习存在三种经典的学习范式，即有监督学习、无监督学习和强化学习。在有监督学习中，知识由样本中所包含的信息和标注信息共同定义，即知识是标注出来的。所以在得到训练样本集$X$后，我们需要对其中每个样本进行标注，使每一个${x}$对应一个（或多个）标签$y\in Y$（离散或者连续）。标注信息给出了从输入空间${\mathcal{X}}$到标签空间（即输出空间）${\mathcal{Y}}$的映射，知识蕴含其中。我们一般将训练过程中完全可见的数据（包括样本和其标签）称为训练集，它给出了较为准确但数量有限的“输入-输出”映射关系，我们会通过让模型拟合这些映射关系来挖掘潜在的数据模式，以完成对知识的学习。一般来说，样本标注需要花费大量的人力物力，标注方式要求专业、严谨、合理，标注信息越准确对知识的定义就越准确，也就越有利于模型学习，因此数据标注是机器学习过程中非常重要的一个环节。当涉及到专业性较强的学习任务时，如标记医疗影像中的病变位置，甚至还需要领域专家的参与和指导。在有监督学习范式下，训练数据集$D$由训练样本集$X \subset {\mathcal{X}}$和其对应的标签集$Y \subset {\mathcal{Y}}$共同构成:

(2.1.3)¶\[% D = \{X,Y\} = \{(\vx_i,y_i)|\vx_i \in X, y_i \in Y\}. D=\{(X,Y)\}=\{({x}_i,y_i)\}_{i=1}^{n}. \label{eq:trainset}\]

除标注信息外，数据本身的分布规律也蕴含了丰富的知识。因此一些机器学习任务要求模型可以从数据中自主挖掘潜在模式，以完成对数据中所蕴含的规律进行学习，这种学习范式称为无监督学习。在这种情况下，标签集合为空集，即$Y=\emptyset$。所以对无监督学习来说，知识是发掘出来的。在有监督学习和无监督学习之间还存在半监督学习范式，在这种情况下数据部分有标注部分无标注。实际上，当无监督数据集被标注以后就可以被转换成为有监督学习任务，虽然这在当前机器学习中并不常见。而有监督学习往往也存在无监督的部分，比如图像分类任务中存在开集类别（open-set class），这在当前机器学习中也是被忽视的。从某种程度上来说，我们大部分的学习任务实际上是半监督的，因为我们总可以对一部分数据进行标注，也总要面对不断出现的未知样本。

在强化学习过程中，智能体在与环境交互的过程中根据奖惩反馈来调整探索策略以最大化奖励。所以对强化学习来说，知识是探索得到的。关于何种知识获取方式，即有监督学习中的人工标注、无监督学习中的自主发掘、或者强化学习中的探索发现，才是定义知识的最佳方式一直是机器学习领域一个争论不休的话题。其中有一部分研究者认为自主挖掘和探索发现才是获取知识的正确方式，也就是无监督和强化学习才是人工智能的未来。然而，很多现实世界中的问题又更适合以有监督学习的方式进行定义，而且有监督学习的学习效率和泛化性能往往要高于无监督学习。与此同时，一些学者尝试使用自监督学习、迁移学习等方式，逐步缩小不同学习范式之间的差异，进而证明同一个问题可以由不同的学习范式同等解决。本章3.2小节将具体介绍这几类经典的机器学习范式。

图2.1.1 机器学习是一种映射学习¶

机器学习的主体往往是人工设计的数学模型。 在获得训练数据之后，机器学习通常会对“输入-输出”映射进行数学建模，并对参数化的模型进行优化。数学模型规定了从输入到输出的具体映射形式，无论是简单的线性模型还是更为复杂的深度神经网络，它们都可以被看作从输入样本到输出目标的函数映射$f$。图图2.1.1 展示了三种不同的学习任务，分别是语音识别、人脸识别和语义分割，主要区别是映射的具体形式。从输入空间${\mathcal{X}}$到输出空间${\mathcal{Y}}$的映射函数可抽象的表示为：

(2.1.4)¶\[{\mathcal{Y}}= f({\mathcal{X}}).\]

值得注意的是，由于不同模型架构具备不同的映射复杂度，在具体问题上存在优化难易的差别，因此需要根据实际问题的特点对数学模型进行合理设计。而模型架构一选定，其对应的映射函数族（function family）也就确定了。所有可能函数的具体形式将共同构成模型的假设空间$\mathcal{F}$，即在模型架构确定的前提下，$\mathcal{F}$为包含了所有可能映射函数的集合：

(2.1.5)¶\[\mathcal{F}=\{f|{\mathcal{Y}}=f_{\theta}({\mathcal{X}}), \theta \in {\mathbb{R}}^m\},\]

其中，$\theta$是参数空间，不同的$\theta$对应不同的函数$f_\theta$。例如，当模型被确定为关于输入变量的线性函数时，模型的假设空间即为所有线性函数构成的集合，线性函数的每一种组合系数$\theta$对应模型假设空间的一个点。当选定模型架构后，我们需要考虑如何获得最优的模型参数，这就需要具体的学习算法来实现参数优化。

机器学习的过程是模型参数优化的过程。 未经学习的模型不包含任何任务相关的知识，更不具备解决实际问题的能力，这时候就需要学习算法的参与。学习算法包含两个核心要素，分别是损失函数和优化策略。对有监督学习任务来说，损失函数定义了模型的预测错误，即模型的输出$f({x})$与真实标签$y$之间的不一致性。所以损失函数通常是一个非负实值函数，通常用$\mathcal{L}(f({x}),y)$来表示。损失函数值越小，一致性越高，模型拟合越好。假设输入和输出是$(X,Y)$的随机变量，服从联合分布$P(X,Y)$，在整个数据分布上的期望损失（expected loss）可定义为：

(2.1.6)¶\[R_{\text{exp}}(f)=\mathbb{E}_P[\mathcal{L}(f({x}), y)]=\int_{X \times Y}\mathcal{L}(f({x}),y)P({x},y)d{x}dy. \label{eq:eloss}\]

学习的目标就是找到使期望损失最低的模型参数$\theta^*$，而在现实场景中$P(X,Y)$是未知的，所以式[eq:eloss]无法直接求解，需要模型通过在训练数据上“学习”来逐步逼近。

在实际机器学习求解过程中，人们通常使用经验风险（empirical risk）来近似期望损失。给定训练数据集$D$（式[eq:trainset]），经验损失可定义如下：

(2.1.7)¶\[R_{\text{emp}}(f)=\mathbb{E}_{({x},y) \in D} \mathcal{L}(f({x}),y) = \frac{1}{n}\sum\limits_{i=1}^{n}\mathcal{L}(f({x}_i),y_i). \label{eq:emp}\]

此处近似的合理性与前文提到的独立同分布采样假设紧密相关。实际优化通常遵循经验风险最小化（empirical risk minimization, ERM）策略，将求解最优模型参数转换为求解下面的最小化问题：

(2.1.8)¶\[\theta^* = \underset{\theta}{\mathop{\mathrm{arg\,min}}} \frac{1}{n}\sum\limits_{i=1}^{n}\mathcal{L}(f_{\theta}({x}_i),y_i) \label{eq:emp_target}.\]

在本书的后续章节中，我们在无歧义的情况下忽略$f_{\theta}$中的$\theta$符号，简单的用$f$来表示模型和模型所代表的函数。

当样本容量足够大时，最小化经验风险往往能够取得很好的学习效果。然而在大部分情况下，训练样本的数量是非常有限的，而且往往存在一些噪声数据，这使得训练数据不能够完全反映真实的数据分布。在这种情况下，通过经验风险最小化得到的模型很容易出现过拟合（overfitting）的现象，即在训练数据集上性能很好，但在测试数据集上性能却很差。为了缓解模型过拟合，结构风险最小化（structural risk minimization, SRM）准则被提出。

我们可以认为过拟合是由于模型过度复杂（拟合能力过强）、训练数据过少、训练数据噪声过多等原因造成的，因此可以通过正则化（regularization）的方式来对模型的参数进行约束，以缓解模型过拟合的问题。常用的正则化方法有$L_1$范数正则化和$L_2$范数正则化，我们用$\Omega(\theta)$来表示模型参数正则化，这两种正则化方法分别表示如下：

(2.1.9)¶\[\label{eq:l1_reg} L_1: \Omega(\theta) = \|\theta\|_1 = \sum\limits_{i} |\theta_i|,\]

(2.1.10)¶\[\label{eq:l2_reg} L_2: \Omega(\theta) = \|\theta\|_2 = \sum\limits_{i} \theta_i^2.\]

在经验风险最小化的基础上引入参数正则化来限制模型的复杂度可有效缓解过拟合现象，而二者的结合则为结构风险，用$R_{\text{srm}}$来表示如下：

(2.1.11)¶\[\begin{split}\begin{aligned} \begin{aligned} R_{\text{srm}}(f) &= R_{\text{emp}} + \lambda \cdot \Omega(\theta) \\ & = \frac{1}{n}\sum\limits_{i=1}^{n}\mathcal{L}(f_{\theta}({x}_i),y_i) + \lambda \cdot \Omega(\theta). \end{aligned} \end{aligned}\end{split}\]

基于结构风险最小化的参数优化目标则为：

(2.1.12)¶\[\theta^* = \underset{\theta}{\mathop{\mathrm{arg\,min}}} \Big[ \frac{1}{n}\sum\limits_{i=1}^{n}\mathcal{L}(f_{\theta}({x}_i), y_i) + \lambda \cdot \Omega(\theta)\Big], \label{eq:srm_loss_min}\]

其中，$\lambda>0$是正则化系数，用于控制正则化的强度，以权衡经验风险和模型复杂度。

在确定好优化目标之后，如何对优化目标进行求解则涉及到学习算法的第二个核心要素：优化策略。优化策略（也称优化方法、优化器）多种多样，光是基于梯度的一阶优化方法就有很多种，如SGD、AdaGrad、AdaDelta、 Adam、RMSProp等。此外还有零阶（黑盒）优化方法，如网格搜索、随机搜索、遗传算法、进化策略等，以及二阶优化方法，如牛顿法、拟牛顿法（如BFGS、L-BFGS）等。模型参数的优化过程也就是模型训练的过程，模型在拟合训练数据的过程中不断更新参数直到达到最优目标。本章3.3小节和3.4小节将分别介绍常用的损失函数和优化算法。

机器学习的目标是训练具有泛化能力的模型。 机器学习过程一般会涉及三种类型的数据集合：训练集、验证集和测试集。这三种数据集模拟了真实环境下的机器学习过程：训练集是为了某个机器学习任务而收集的数据，代表过去的经验；验证集是我们在训练过程中选择最优模型的评判依据，代表我们认为的任务环境；测试集是模型在部署后接收到的“未知样本”，代表真实的任务环境。训练集用来训练模型；验证集不参与训练，只用于模型验证和超参选择；测试集在训练过程中严格不可见，用于评估模型的最终泛化性能。数据的独立同分布假设保障了在训练数据上训练得到的模型可以泛化到测试集。值得一提的是，当前有研究者也在尝试探索模型在这种假设之外的分布外（out of distribution，OOD）泛化能力，即当训练数据和测试数据具有相似但不同的数据分布的情况下如何提升模型的泛化能力。

当模型训练完成后，我们需要在测试集上来评估模型的泛化性能。根据模型在训练集和测试集上的不同表现，学习结果可大致分为：适拟合（a good fit）、欠拟合（underfitting）和过拟合（overfitting）。适拟合是指模型在训练集和测试集上的性能差别不大，即模型具有良好的泛化性能；欠拟合是指模型没有充分的学习到数据中包含的特征，模型在训练数据集上的性能就比较差；过拟合是指模型在训练集上效果很好，但在测试集上出现性能大幅下滑。解决欠拟合问题需要适当增加模型复杂度或让训练更充分，如降低正则化惩罚强度、提高模型复杂度、增加模型参数、增加训练周期等。解决过拟合问题则需要调高正则化强度、降低模型复杂度、减少模型参数、使用数据增广、使用早停法（early stopping）等。值得思考的是，当前机器学习社区所讨论的拟合、欠拟合和过拟合都是基于特定数据集来说的，而从知识的角度来说，模型（比如深度神经网络）到底是欠拟合还是早已过拟合尚未可知。

以上从学习任务、知识来源、学习主体、学习算法以及学习目标五个方面介绍了对机器学习的基本概念。下一节将对几种常见机器学习范式进行更详细的介绍。

2.2. 学习范式¶

2.2.1. 有监督学习¶

假设存在一个包含$n$个样本的数据集$D=\{{x}_i,y_i\}_{i=1}^{n}$，其中${x}_i \sim X \subseteq {\mathbb{R}}^{d}$是一个从$d$维输入空间${\mathcal{X}}$中采样得到的样本，$y_i \in Y$是样本${x}_i$的真实标签（输出空间${\mathcal{Y}}$可能是离散的也可能是连续的）。给定数据集$D$，有监督学习的目标是学习一个从输入空间到输出空间的映射函数:$f: {\mathcal{X}}\rightarrow {\mathcal{Y}}$。在有监督学习过程中，我们在数据集$D$上训练模型$f$，使其在每个样本${x}$上的预测值$f({x})$都尽可能的接近真实标签$y$，而此训练过程就是最小化模型在数据集$D$上的经验风险的过程。有监督学习可定义如下：

(2.2.1)¶\[\min_{\theta} \mathbb{E}_{({x},y) \in D} \mathcal{L}(f({x}),y), \label{eq:suplearn}\]

其中，$\theta$表示模型$f$的参数，$\mathcal{L}(f({x}), y)$为损失函数，定义了模型输出与真实标签之间的差距。损失函数值越小,说明模型对数据集$D$的拟合越好（但可能会过拟合）。

根据输出变量$Y$的类型，有监督学习问题又分为分类问题和回归问题。在分类问题中，输出变量$Y$的取值范围为有限个离散值组成的集合，每个离散值是一个“类别”。解决分类问题的模型包括随机森林、支持向量机、深度神经网络等。在回归问题中，输出变量$Y$为连续型变量，学习一个回归模型等价于拟合一个从输入变量映射到输出变量的函数。解决回归问题的模型包括线性回归模型、逻辑回归模型、深度神经网络等。实际上，很多机器学习模型既可以用于分类问题也可以用于回归问题，并没有严格的界限，分类与回归问题也大都可以相互转换。

作为一种统计学习任务，有监督学习要求模型具有对未知数据的良好泛化性能，因此过拟合是有监督学习必须要面对的问题。前文提到过解决过拟合的一些方法，如使用基于$L_2$范数的权重衰减（weight decay）（式[eq:l2_reg]）、使用数据增广、使用早停法等。正则化是这些方法的核心，如数据增广、随机失活（dropout） (Srivastava et al., 2014) 等都可以被理解为是一种正则化。实际上，提升模型泛化性的最好方法往往是简单粗暴的增加训练数据。此外，在训练数据已确定的情况下，我们还可以使用各种数据增广（data augmentation）方法来丰富训练数据。数据增广相当于对训练样本进行某种变换来产生新的样本$t({x})$，一般不改变类别$y$。对图像数据来说，常用的数据增广方法有翻转、旋转、裁剪、缩放、颜色变换、Cutout (DeVries and Taylor, 2017) 、Mixup (Zhang et al., 2018) 、Cutmix (Yun et al., 2019) 、AutoAugment (Cubuk et al., 2019) 等。此外，向输入中添加随机或者特定的噪声也是一种常见的数据增广方式。

对有监督学习来说，数据的标签类型和标注准确率会对模型最后的性能产生很大的影响。对于分类任务来说，类别越多任务也就越难，类别越复杂任务也会越难，比如从单标签分类问题到多标签分类问题。此外，虽然我们使用的很多数据集都是人工标注的，但是由于标注的困难（比如标记1000个类别），这些数据集难免会存在一些标注错误，给模型的训练带来一定挑战。这个问题也称为噪声标签（noisy labels）问题。噪声标签问题在一些大规模数据集如ImageNet (Deng et al., 2009) 和COCO (Lin et al., 2014) 上普遍存在。同样的，测试数据集中也可能会存在噪声标签，会给模型的性能评估带来一定的不准确性。

2.2.2. 无监督学习¶

无监督学习是机器学习的另一类重要学习范式。无监督学习要求算法能够在没有标注的数据上进行自主学习，充分发掘数据本身的性质和内在的关联关系。这一抽象过程可以被描述为：设计算法$A$作用于样本集合$X$得到函数（模型）$f$，所得到的模型$f$将最终作用于数据本身$X^*$（$X \subseteq X^*$）得到某种分析结果$r$。该过程可以抽象描述为：

(2.2.2)¶\[\begin{split}\begin{aligned} \begin{aligned} &\text{步骤 1: }A(X) \rightarrow f ;\\ &\text{步骤 2: }f({x}\in X^*) \rightarrow r. \end{aligned} \end{aligned}\end{split}\]

相比于有监督学习，无监督学习最大的不同在于步骤1只使用了数据集$D$中的样本$X$本身，没有标注信息$Y$，算法仅通过分析数据自身特性就能学习得到分析函数$f$，完成对数据集自身的分析（步骤2）。所分析的数据$X^*$可能是已见过的学习样本，也可能是未见过的样本点，而分析的结果$r$由具体任务决定。常见的无监督学习任务有聚类分析、相关性分析、特征降维、异常检测、对比学习、数据重建等。针对不同的无监督学习任务，我们需要设计不同的算法$A$对数据进行分析，这些方法从不同的角度解决同一个核心问题，即如何在无显式标注的情况下实现“自我监督”。

聚类分析（clustering）是一类经典的无监督学习任务，目的是将空间中的数据点按照某种方式聚为对应不同概念的簇（cluster）。簇内距离和簇间距离是衡量聚类方法性能好坏的核心标准，这需要由一个距离度量（distance metric）来定义。实际上，将很多数据点聚成几类很容易，但是要每一个类簇都有不同的意义则很难，更何况很多时候我们无法知道到底应该有几个簇。经典的聚类算法包括k-means (Hartigan and Wong, 1979) 、DBSCAN (Ester et al., 1996) 等。从某种程度上来说，分类问题是聚类问题的一个简单版本，类簇是已知的且预先标记好的。聚类分析与特征学习也有着密切的关联，研究表明深度神经网络强大的特征学习能力将有助于发现更准确的类簇 (Caron et al., 2018) ，可以先学特征再聚类或者边学特征边聚类。一般来说，聚类模型不易受少量异常数据点的干扰，安全性要高于分类模型。

特征降维（dimensionality reduction）是无监督学习中的另一类重要任务，其目的是将高维数据映射到低维空间，用更少维度的特征来替代原始高维度特征，同时最大限度的保留高维特征所包含的信息（即方差），从而达到降低时间复杂度、提高数据分析效率、防止模型过拟合的目的。经典的降维方法包括主成分分析（principal components analysis，PCA） (Jolliffe, 2002) 、t-SNE（t-distributed stochastic neighbor embedding） (Van der Maaten and Hinton, 2008) 等。其中，PCA是一种最常用的方法，它通过最大化投影方差来生成一系列线性不相关变量（即主成分），将高维数据映射到低维空间。原先的 $n$ 个特征被更少的$m \ll n$个特征取代，新特征是旧特征的线性组合，PCA算法尽量使新的$m$个特征互不相关以便存储更多的信息。此外，数据在降维的同时会去除一部分噪声，将有利于发现数据中的潜在模式。

自监督对比学习（self-supervised contrastive learning）是无监督学习的一种，其通过对比的手段学习样本间的相同和不同特征，从而得到高效的特征抽取模型$f$，能够对输入样本提取具有判别性的有用特征。对比学习的核心思想在于让“相似”的样本在特征空间更近，让“不相似”的样本在特征空间更远。例如，我们可以将相同实例的不同视角（如应用不同的数据增强）视为相似样本（也称正样本对），同时将不同的实例视为不相似样本（也称负样本对）。此外，还可以利用聚类方法，将同一个簇内的样本定义为相似样本，而来自不同簇的样本则视为负样本对。目前，如何设计合理的对照和相似性度量是自监督对比学习研究的重点 (Tian et al., 2020) 。

数据重建（data reconstruction）通过重构原始样本来学习数据的有效表示或者学习生成特定分布的样本。基于自我重建的无监督学习包含了很多经典的算法，如自编码器（autoencoder） (Rumelhart et al., 1986) 、变分自编码器（variational autoencoder，VAE） (Kingma and Welling, 2013) 、生成对抗网络（GAN） (Goodfellow et al., 2014) 等。自编码器的目的是学习数据的有效编码，其通过一个编码器（encoder）将样本压缩成一个潜在空间表示，然后通过一个解码器（decoder）将空间表示重构为输入样本。变分自编码器则是将输入编码为隐空间中的分布，并基于隐空间中采样得到的特征点来重建输入，以此来学习一个能够建模真实数据分布的生成模型。生成对抗网络是一种非显式建模数据分布的生成模型，其特点是通过一个判别器（discriminator）和一个生成器（generator）之间的对抗学习来促使生成器生成符合真实数据分布的样本。在生成对抗网络中，两个模型（即判别器和生成器）的目标相反，其中判别器 $D$ 的目标是判断一个样本是否为生成器生成，而生成器$G$的目标则是尽可能生成判别器无法判断真假的样本。交替训练这两个相互对抗的模型可以使二者达到一个均衡状态（纳什均衡），在此状态下生成器将能够生成符合真实数据分布的样本。

如我们在章节3.2.1提到的，现实世界的学习任务是复杂多样的，在有监督和无监督之间存在一些如半监督学习和弱监督学习等中间类型的学习范式。在半监督学习中，我们将面临输入数据部分被标记，部分未被标记的情况；而在弱监督学习中，我们将面临数据集的标签是不可靠的情况，而这种不可靠性包括了噪声标记、不完整标记、局部缺失标记等。现实场景中，半监督和弱监督任务非常常见，学习算法也非常多样，经常会融合有监督和无监督的各自优势来解决半监督和弱监督学习问题。

2.2.3. 强化学习¶

强化学习（reinforcement learning，RL）的目标是在不确定的复杂交互环境下训练智能体学会从环境中最大化累计奖励。与有监督和无监督学习不同，强化学习通过奖励信号来获取环境对智能体动作的反馈，得到的结果可能具有一定的延时性，即奖励信号的反馈可能会滞后于决策时间。除此之外，在强化学习的决策过程中，每个样本并非一定是独立同分布的，而是具有时序性的序列。在强化学习中，有两个对象进行交互：智能体和环境。强化学习中的一些基本概念如下：

智能体（agent）可以感知外界环境的状态并得到环境反馈的奖励，并在此过程中进行决策和学习。具体来说，智能体根据外界环境的状态产生不同的决策，做出相应的动作，并根据外界环境反馈的奖励来学习调整策略。

环境（environment）是指智能体所处的所有外部事物，其状态受智能体动作的影响而改变，并能根据智能体的动作反馈相应的奖励。

状态（state）是对当前环境信息的总结描述，可被智能体所感知并产生相应动作。状态可以是离散的或连续的，所有状态$s$的集合称为状态空间$S$。在强化学习过程中，智能体往往无法直接获得环境的全部信息，只能通过感知环境的状态，并基于一连串的状态来进行决策和学习。

动作（action）是对智能体行为的描述，智能体的动作可以影响下一时刻环境的状态。动作可以是离散的或是连续的，所有动作$a$的集合称为动作空间$A$ 1。

策略（policy）是一个行为函数，表示在当前环境状态$s$下，智能体如何决定下一步的动作$a$。策略可以分为确定性策略和随机性策略两种。其中确定性策略表示为状态空间到动作空间的映射函数$\pi: S \rightarrow A$，随机性策略表示在某一状态下$s$，智能体以一定概率$\pi(a\mid s)$选择动作.

状态转移概率（state transition probability）是指在状态$s$下，智能体做出动作$a$之后，在下一时刻环境状态转变为状态$s'$的概率$p(s'\mid s,a)$。

奖励（reward）是指智能体在某个状态$s$下执行某个动作$a$之后从环境中获取的即时奖励$R(a,s)$。这个奖励也通常与环境下一时刻的状态有关，即$R(a,s,s')$。

马尔可夫决策过程（Markov decision process，MDP）可以用来表示智能体与环境交互的过程，即一个智能体（agent）采取行动（action），从而改变状态（state）与环境（environment）发生交互并获取奖励（reward）的循环过程。在马尔可夫过程中，下一个时刻的状态$s_{t+1}$只取决于当前状态$s_{t}$，即

(2.2.3)¶\[p(s_{t+1}\mid s_{t},\ldots,s_0) = p(s_{t+1}\mid s_{t}).\]

马尔可夫决策过程在此基础上又引入了动作这一变量，使得下一时刻的状态$s_{t+1}$和当前状态$s_t$以及动作$a_t$相关。

(2.2.4)¶\[p(s_{t+1}\mid s_{t},a_t,\ldots,s_0,a_0) = p(s_{t+1}\mid s_t,a_t).\]

回报（return）和值函数（value function）对于强化学习任务有一个统一的目标：最大化从某一时刻$t$到未来的回报$G_t$，又称累计折扣奖励（cumulative discounted reward）：

(2.2.5)¶\[G_t = \sum_{t}^{\infty}\gamma^t R(a_t, s_t, s_{t+1}),\]

其中，$\gamma^t \in[0,1)$是一个折扣率（discount rate），逐渐降低未来事件的权重。因为策略和状态转移往往具有一定的随机性，每次试验得到的轨迹是一个随机序列，其收获的总回报也并非是确定值。因此，强化学习的目标是学到一个策略$\pi_{\theta}$，根据当前的状态$s$，最大化期望累积奖励（expected cumulative reward），即下面的值函数（value function）：

(2.2.6)¶\[V_{\pi_{\theta}}(s) = \mathbb{E}_{\pi_{\theta}}(G_t|s_t=s).\]

这种状态对应的值函数也称为状态值函数（state-value function）。

根据是否依赖环境模型，强化学习方法可以分为有模型（model-based）和无模型（model-free）两类。二者最大的区别是智能体是否可以直接获得环境的状态转移概率。有模型强化学习具有环境的直接建模（如状态转移概率和值函数），智能体在做出一个动作后可以明确的知道下一个状态$s_{t+1}$（及其对应的奖励）。智能体通过与环境交互来感知环境模型（或学习对环境建模）并探索最优策略。但是现实世界的问题往往存在很多未知和潜在的影响因子，无法对环境进行精确建模。无模型强化学习没有直接的知识或环境模型，而是需要智能体与环境交互来学习价值函数或策略函数，主要是基于大量的试错进行学习，所以相比有模型的强化学习来说，往往需要与环境进行更多的交互。

强化学习算法还可以根据生成样本的策略分为：同策（on-policy）算法和异策（off-policy）算法两类。一般来说，强化学习算法利用目标策略（target policy）和行为策略（behavior policy）来分别完成利用（exploitation）和探索（exploration）两个核心目标。行为策略用来与环境互动产生数据（样本），而目标策略在行为策略产生的数据中不断学习最优的决策策略（即最大化值函数）。在同策算法中，行为策略与目标策略相同，即算法只能使用当前正在优化的策略生成的数据来进行训练。而在异策算法中，用于生成样本的行为策略跟目标策略是分开的，即二者是两个不同的策略，这样可以进行更充分的探索，更容易寻找到全局最优解。实际上，同策算法可以看做是异策算法的特例，即“行为策略=目标策略”的特例。相较而言，异策算法的优势是更为强大和通用，劣势是收敛慢，原因是它确保了数据的多样性和行为覆盖的全面性。

2.2.4. 其他范式¶

有监督学习、无监督学习和强化学习是机器学习的三种基本范式。除此之外，为了应对复杂多样的应用场景需求，也衍生出了很多其他的学习范式。这些范式在数据的获取方式、学习环境、资源分配、应用需求等方面各不相同，但大都是上述三种基本范式的变形、改进或组合。下面简单介绍几种比较常见的其他范式。

迁移学习（transfer learning）是在目标任务数据不足的情况下，充分利用其他学习任务的已有模型，将其强大的特征学习能力迁移到目标任务的学习算法。迁移学习的本质是通过源域（source domain）知识来辅助学习目标域（target domain）知识。源域（或源任务）数据集被称为源数据集$D^s=\{{x}^s_i,y^s_i\}_{i=1}^{n^s}$，目标域（或目标任务）数据集被称为目标数据集$D^t=\{{x}^t_i,y^t_i\}_{i=1}^{n^t}$。在一个机器学习任务里，数据、特征和模型承载了主要的知识，都有可能成为迁移学习的对象。所以根据迁移对象的不同，迁移学习算法又分为样本迁移、特征迁移、模型迁移等不同类别。

样本迁移适用于源域和目标域存在一定的类别重叠的情况，目标是通过重用源域样本来提升迁移性能。常用的方法是为源域样本赋予不同的权重，通过提升源域中有利于目标域任务的样本的权重，同时降低不利于目标域任务的样本的权重，以此来增强模型在目标域任务上的性能。但这类方法通常只在领域间分布差异不大时有效，对于计算机视觉、自然语言处理等任务效果并不理想。

特征迁移的应用更为广泛，它适用于源域和目标域特征空间不一致的场景。常见的解决思路有如下两种：（1）从特征空间出发，利用分布距离度量或使用对抗学习，缩小模型提取的源域特征和目标域特征的分布差异；（2)从输入空间着手，将源域数据变换到目标域进行学习，以完成跨领域泛化。这两类解决思路可形式化定义如下：

(2.2.7)¶\[\begin{split}\begin{aligned} \left\{ \begin{aligned} \text{Type 1: } & \min_{\theta} \Big[\mathbb{E}_{({x},y) \in D^s} \mathcal{L}(f({x}),y) + \mathcal{L}_{\text{dis}}(g(D^s),g(D^t)\Big], \\ \text{Type 2: } & \min_{\theta} \mathbb{E}_{({x},y) \in D^s} \mathcal{L}{(f \circ X_{s \rightarrow t}({x}),y)}, \\ \end{aligned} \right. \end{aligned}\end{split}\]

其中，$f=h \circ g$为任务模型，$h$为任务头，$g$为特征编码器，$\theta$为模型参数，$\mathcal{L}(f({x}),y)$对应任务损失函数，$g(D)$为数据集$D$的样本特征集合，$\mathcal{L}_{\text{dis}}(\cdot,\cdot)$为衡量特征集合分布差异的函数，指导两个域之间的特征对齐。可以看出，第一类方法会增加额外的损失项（$\mathcal{L}_{\text{dis}}$）来约束特征编码器，使其学习到不同领域之间的共同模式；而第二类方法需要首先学习将数据从源域转换到目标域的转换映射$X_{s \rightarrow t}$，比如通过神经网络进行学习，以此来降低域间差异，提升模型泛化能力。

除了样本迁移和特征迁移，模型迁移是另一类被广泛研究的迁移方法，它通过找到源域和目标域之间可以共享的模型参数信息，以此最大化利用在源域数据上预训练的模型的知识。在深度学习中，一种常见的模型迁移方法是利用大规模预训练模型对下游任务模型进行初始化，然后以微调（或者添加特定任务模块后再微调）的方式完成预训练模型到下游任务的跨域迁移。模型迁移可形式化表示如下：

(2.2.8)¶\[\begin{split}\begin{aligned} % \left\{ \begin{aligned} & \min_{\theta \subset \theta_g \cup \theta_{h^t}} \mathbb{E}_{({x},y) \in D^t} \mathcal{L}^{t}(h^t \circ g({x}),y) \\ & \theta_{\text{init}} = \mathop{\mathrm{arg\,min}}_{\theta} \mathbb{E}_{({x},y) \in D^s} \mathcal{L}^{s}(h^s \circ g({x}),y), \\ \end{aligned} % \right. \end{aligned}\end{split}\]

其中，$g$表示预训练特征抽取器，$h^s$和$h^t$分别表示源（预训练）任务和目标任务头，$\mathcal{L}^{s}$和$\mathcal{L}^{t}$分别表示源任务和目标任务的损失函数，$D^s$和$D^t$分别表示源数据集和目标数据集。实际上，模型迁移的实现方式有很多种，比如可以固定住网络深层结构而更新浅层结构，也可以借助后面要介绍的知识蒸馏技术，让下游任务模型能够学到源域模型中更多的知识。人工智能安全研究非常注重迁移性，例如攻击和防御方法能否迁移到不同的数据集、模型结构、训练方式等；亦或是利用特征迁移技术提升模型的通用防御能力。

在线学习（online learning）是与离线学习相对的概念，是指训练数据或者学习任务是在模型的部署使用过程中不断更新或增加的，需要持续优化模型以满足动态增长的需求。前面介绍的很多学习方法都是离线学习方法，即训练数据是预先收集好的。而在线学习要求数据按顺序可用，利用新到来的数据实时的对模型参数进行更新和优化。其中增量学习是一种典型的在线学习范式，它要求模型能够不断地处理现实世界中新产生的数据流。新旧知识之间存在一定的权衡，所以增量学习的难点是如何让模型在吸收新知识的同时能够最大化的保留甚至整合、优化旧知识。

我们将增量发生之前的数据称为旧数据集，定义为$D_{\text{old}}=\{{x}_i^{\text{old}}, y_i^{\text{old}}\}_{i=1}^{n_{\text{old}}}$，而新增加的数据集则定义为$D_{\text{new}}=\{{x}_i^{\text{new}}, y_i^{\text{new}}\}_{i=1}^{n_{\text{new}}}$。增量学习的优化目标可定义如下：

(2.2.9)¶\[\min_{\theta} \big[\mathbb{E}_{({x},y) \in D_{\text{old}}} \mathcal{L}(f({x}),y) + \mathbb{E}_{({x},y) \in D_{\text{new}}} \mathcal{L}(f({x}),y)\big],\]

其中，$\theta$表示模型$f$的参数，$\mathcal{L}(f({x}), y)$为损失函数。可以看出，增量学习的优化目标是让模型能够在新旧两个数据集上的期望损失最小。然而，在增量学习过程中，新旧数据无法同时可见，模型先可见旧数据，后可见新数据，在新数据上进行学习的过程中旧数据又变为不可见或少部分可见，这会导致模型发生灾难性遗忘（catastrophic forgetting）。一般可以通过增加参数约束项、预保存旧数据的少量关键特征（并在增量过程中进行回放）、对模型重要参数进行冻结等方式来解决。

联邦学习（federated learning，FL）是针对数据孤岛现象所提出的一种多方协同学习（collaborative learning）技术。在当今信息时代，数据是宝贵的资源，机器学习（尤其是深度学习）往往需要大量数据来训练高性能的模型。然而在实际场景中，不同的机构虽然都拥有一部分的私有数据，但往往由于各种限制无法共享，这就导致个体机构能利用的数据量是非常有限的，难以整合产业优势。这种现象被形象地称为“数据孤岛”，指不同业务系统之间无法协同互通的状态。尽管随着5G通信和物联网技术的快速发展，大量的数据被不断的采集，但是数据孤岛现象却日益严重，所带来的问题包括：如何安全分享信息、如何有效利用异构数据、如何快速传输交付、如何定价数据价值等。在数据孤岛问题之下，联邦学习应运而生，其允许各方在不共享数据的情况下可以联合训练一个强大的全局模型。

联邦学习存在多个参与方和一个中心参数服务器，每个参与方有自己的数据和模型，可以进行本地模型训练，各参与方在一定次数的本地训练后将本地模型参数上传至中心服务器，中心服务器根据聚合本地参数后更新全局模型，各参与方下载全局模型并继续进行本地训练，以此往复直至全局模型收敛。由于只是共享模型参数（或梯度信息）而不需要共享数据，联邦学习也通常被认为是一种“隐私保护”（privacy-preserving）的学习范式。根据各方私有数据的分布类型不同，联邦学习又可以分为横向联邦学习(horizontal federated learning，HFL）和纵向联邦学习（vertical federated learning，VFL）。如果以一个包含若干行和列的数据表为例，横向联邦中各参与方拥有不同的“数据行”，而纵向联邦各参与方拥有不同的“数据列”。它们共同需要面对的挑战包括：非独立同分布（non-IID）的数据、有限通信带宽、不可靠或有限的设备等。关于联邦学习及其安全问题将会在章节6.3和章节9.5分别进行详细的介绍。

知识蒸馏（knowledge distillation，KD）是将知识从一个大的教师模型中蒸馏到一个小的学生模型中的学习方法。知识蒸馏在资源受限的移动端部署中具有重要的应用价值，可用于训练服务于图像分类、目标检测、语义分割等任务的高效小模型，甚至在对抗防御中也有重要的应用。蒸馏的核心思想是对齐，通过让学生模型的逻辑或概率输出对齐教师模型以达到知识蒸馏的目的，对齐也可以理解为是一种“模仿学习”，因此所有以“对齐”为主的训练方式都可以叫蒸馏。蒸馏得到的学生模型一般比从头训练（training from scratch）具有更好的性能。令学生模型为$S$，教师模型为$T$，$\mathcal{L}_{\text{sim}}$表示两个模型输出的一致性约束，给定数据集$D=\{{x}_i,y_i\}_{i=1}^{n}$，知识蒸馏的优化目标可定义如下：

(2.2.10)¶\[\min_{\theta_s} \mathbb{E}_{({x},y) \in D} \mathcal{L}_{\text{sim}}(S_{\theta_s}({x}), T_{\theta_t}({x})).\]

知识蒸馏技术在数据与模型安全中的很多地方都有涉及。比如，蒸馏技术可以用来从一个已训练的模型中逆向工程原始训练数据，以达到数据窃取的目的。再比如，在模型防御方面，可以通过鲁棒性蒸馏技术将鲁棒性从教师模型迁移到结构更为简单的学生模型，以弥补小模型在鲁棒训练方面的不足。

多任务学习（multi-task learning, MTL）是指通过单个模型完成多个任务的学习范式。有别于单任务学习，多任务学习把多个紧密相关的任务放在一起进行学习，建立任务间的共享表征，从而提高模型在多个任务上的同时泛化能力。单任务学习必须对每个任务训练一个模型，在多任务推理时还需要进行二次组合或相互调用，而多任务学习得到的模型可以同时完成多个任务的推理，有效减少训练和推理时间。章节 3.2.1中所介绍的有监督学习就是一种单任务学习，我们在其基础上进行多任务的扩展。定义数据集$D=\{{x},y\}_{i=1}^{n}$，其包含$m$个子任务$\{T_i\}_{i=1}^{m}$，多任务学习的目标是在同一个输入上完成多个不同的子任务，如对一张图片同时进行目标检测和图像分割。一种常见的多任务建模方式是使用一个共享表征模型$g$对输入进行特征编码，进而针对$m$个不同的任务设计不同的任务头$\{h_i\}_{i=1}^m$。多任务有监督学习往往要求模型对多个子任务同时进行优化，每个任务对应一个损失函数$\mathcal{L}_i$，可以根据学习的难易程度赋予不同的任务以不同的权重。多任务学习的目标可形式化表示如下：

(2.2.11)¶\[\min_{\theta} \mathbb{E}_{({x},y) \in D} \sum_{i=1}^{m} w_i \cdot \mathcal{L}_i(h_i\circ g({x}),y).\]

多任务学习的安全性问题是一个尚未充分探索的开放研究领域。在攻击方面，可以探索如何设计能够同时攻破多个任务的通用攻击方法、如果根据一个任务来破坏其他任务等；在防御方面，可以探索能防御多任务攻击的高效防御方法、如何高效利用多任务互补信息来建立更完备的防御框架等。

小样本学习（few-shot learning，FSL）是一种以有监督学习为主，仅依赖少量样本就可以高效学习和泛化的学习方法。人类可以根据已有经验，仅凭少量样本就可以辨识新的事物，而小样本学习的出现，就是为了让机器也可以拥有类似的能力。小样本学习一般定义为一个$C$-way-$K$-shot的任务，$C$-way指$C$个类别，$K$-shot指每个类别包含$K$个样本。学习设计三种数据集：训练集、支撑集（support set）和查询集（query set）。任务要求在训练集上训练的模型能够以$C*K$个已知标签的样本作为支撑集，快速准确地学习新的类别概念，并在查询集（测试时未知标签的数据构成的集和）上达到很好的表现。这种通过少量样本快速学习的能力往往需要模型从更多的数据中获取先验知识，因此，小样本任务往往会提供与测试语义相关但不相同的训练数据$D=\{{x}_i,y_i\}_{i=1}^{n}$，保证标签空间不相交。

解决小样本学习问题最简单的方法是让模型先在训练集上进行充分训练，然后在测试支撑集上进行二次训练，最后在测试查询集上进行性能评测。另一类常见的方法则是引入元学习（meta learning）的思想：让模型学会如何学习（learning to learn）。具体来说，这类方法视训练集上的每一次训练迭代为一次小样本学习过程，仿照测试阶段$C$-way-$K$-shot的方式将每个小批量训练数据划分为支撑集$D_i^{\text{sup}}=\{({x}^{\text{sup}}_i,y^{\text{sup}}_i)\}$和查询集$D_i^{\text{query}}=\{({x}^{\text{query}}_i, y^{\text{query}}_i)\}$，并确保支撑集$D_i^{\text{sup}}$包含$C*K$个样本。我们将每种划分定义为任务$T_i$，其对应数据集$D_i=D^{\text{sup}}_i \cup D^{\text{query}}_i$，于是总的训练任务为$T_{\text{train}}=\{T_1, \ldots, T_n\}$，总的训练集为$D_{\text{train}}=\{D_1, \ldots, D_n | D_i \subset D\}$，并通过如下公式训练模型：

(2.2.12)¶\[\min_{\theta}\mathbb{E}_{D_i \in D_{\text{train}}} \mathbb{E}_{({x},y) \in D^{\text{query}}_i} \mathcal{L}(f(D_i^{\text{sup}},{x}),y).\]

与普通有监督学习任务相比，小样本学习的挑战来源于模型需要在新任务上以很少的训练样本量完成学习，并在大量样本上进行测试。因此小样本学习容易对已有数据产生依赖过度，容易受数据投毒、后门攻击等数据相关的攻击威胁。从防御安全的角度来说，目前最为有效的对抗防御手段需要在线构造大量对抗样本进行对抗训练，然而小样本学习在迁移到新任务的过程中每个类别仅有少量标注样本，难以进行大量对抗训练，因此在小样本任务下如何训练对抗鲁棒模型仍是一个充满挑战的问题。

通过前面的介绍可以看出，机器学习范式多种多样，不同学习范式下数据采集与使用方式、模型训练流程、学习目标、优化算法、以及最终模型的部署形式等不尽相同，所面临的安全问题和需要的防御方法也会有一定差异。这也是当前人工智能安全问题多样化的主要原因。虽然目前人工智能安全研究主要围绕有监督学习进行研究，相信未来这些研究将会扩展到更多样化的学习范式和实际应用场景中去。

2.3. 损失函数¶

给定一个学习任务，损失函数定义了具体优化的目标。我们需要根据任务的具体形式和特点设计合理的损失函数$\mathcal{L}(f({x}), y)$以评估模型预测值和真实值之间的不一致程度；而优化的过程则以最小化损失函数定义的经验错误为目标，通过特定的优化策略对模型参数进行更新，不断减小模型输出与真实值之间的不一致性。对于不同的任务来说，优化的目标变量也各不相同，对于一般的模型训练来说，优化变量为模型参数，而对于很多攻击算法来说优化的变量是输入扰动（噪声），因为其要修改输入以使模型犯错。下面将基于深度神经网络介绍几种经典学习任务中经常使用的损失函数，当然这些任务也跟数据和模型安全密切相关，很多攻击和防御方法需要基于这些任务进行研究。

2.3.1. 分类损失¶

交叉熵（cross-entropy，CE）损失无疑是最广泛使用的分类损失函数。在信息论中，交叉熵用来衡量两个概率分布之间的差异性。给定两个概率分布$q$和$p$，我们常用$H(q,p)$表示分布$p$相对于分布$q$在给定集合上的交叉熵，具体定义为$H(q,p)= -\sum\limits_i q_i \log p_i=-\mathbb{E}_q[\log p]$。在机器学习领域，标签和模型输出往往是多维向量（如独热编码），所以我们用粗体${q}$表示真实标签分布，粗体${p}$表示模型预测分布，而交叉熵则衡量了预测分布和真实分布之间的差异。

在单标签分类问题中，每个样本${x}$只属于一个正确类别$y$。假设类别总数为$K$，对于输入样本${x}$及其标签$y$，模型$f$的预测概率输出为$f({x})={p}\in \mathbb{R}^K$（$K$维的概率向量，每个维度对应一个类别，$\sum_{k=1}^{K}{p}_k=1$），交叉熵损失定义如下：

(2.3.1)¶\[\mathcal{L}_{\text{CE}}(f({x}),y) = -{y}\log({p}) = -\log({p}_{y}), \label{eq:celoss}\]

其中，${y}$为类别$y$的独热编码，${p}_{y}$为模型输出的概率向量中类别$y$所对应的概率。当类别数量为2（即$K=2$）时，多分类任务退化为二分类问题。对于二分类问题，如果模型的输出维度为2，则仍可以用式 [eq:celoss] 来计算交叉熵损失。但很多时候人们会将模型的输出维度调整为1，并选择Sigmoid函数转换获得最终的概率，以保证$f({x})=p\in [0,1]$。此时定义的交叉熵损失也被称为二元交叉熵损失（binary Cross-entropy, BCE），定义如下：

(2.3.2)¶\[\mathcal{L}_{\text{BCE}}(f({x}), y) = y \cdot \log(p) + (1-y) \cdot \log(p).\]

分类任务除单标签场景外还存在多标签分类场景，即每一个样本可能对应一个或多个标签。单标签可用独热编码${y}$来表示类别标签$y$，即${y}_{k=y}=1$且${y}_{k\neq y}=0$。而在多标签场景下，独特编码就变成了多热编码（multi-hot encoding），每个标签对应的位置都是1。多标签分类问题可以被转换为多二分类问题，此时交叉熵损失可以定义如下：

(2.3.3)¶\[\mathcal{L}_{\text{CE}}(f({x}), {y}) = \sum\limits_{k=1}^{K} \mathcal{L}_{\text{BCE}}({p}_k, {y}_k).\]

在实际应用场景中，数据的标注质量往往无法保证，由于标注任务的复杂性，导致即便高质量的数据集（如ImageNet）也难免会存在噪声（错误）标签。错误标注的样本会误导模型往错误方向优化，降低模型的最终性能。近年来，研究者提出了一些鲁棒分类损失函数，可以在一定程度上提高训练过程对噪声标签的鲁棒性。下面将介绍几个此类的鲁棒损失函数。

广义交叉熵（generalized cross-entropy，GCE） (Zhang and Sabuncu, 2018) 是对平均绝对误差（mean absolute error，MAE）和交叉熵损失的泛化，综合了CE的隐式加权特性和MAE对噪声标签的鲁棒性 (Ghosh et al., 2017) 。考虑单标签分类场景，广义交叉熵损失定义如下：

(2.3.4)¶\[\label{eq:gce} \mathcal{L}_{\text{GCE}}(f({x}), y) = \frac{(1-{p}_y^{\gamma})}{\gamma}, \;\; \gamma \in \text{(0,1]},\]

其中，$\gamma$为超参数。当$\gamma$趋于0时，根据洛必达法则（L$'$Hôpital$'$s rule），式 [eq:gce] 上下求导，GCE将退化为CE损失函数；而当$\gamma=1$时，GCE则退化为MAE，因此可以认为GCE损失是CE和MAE更广义的定义。

对称交叉熵（symmetric cross-entropy，SCE）是另一个常用的鲁棒损失函数，其在交叉熵损失的基础上增加了一个逆交叉熵（reverse cross-entropy，RCE）损失，一起形成了一种对称结构（故称”对称交叉熵”）。设${q}$为真实标签分布，${p}$为模型预测概率分布，交叉熵损失定义为$H({q}, {p})=-{q}\log {p}$，而逆交叉熵损失则定义为$H({p}, {q})=-{p}\log {q}$（注意${p}$和${q}$的顺序相对交叉熵发生了调换）。SCE损失是交叉熵和逆交叉熵的加权组合，定义如下：

(2.3.5)¶\[\mathcal{L}_{\text{SCE}}(f({x}),y) = -\alpha \cdot {y}\log {p}- \beta \cdot {p}\log {y},\]

其中，$\alpha$和$\beta$为两个超参数，平衡两个损失项；${y}$为真实标签的独热编码，需要将其零值替换为一个很小的数值（如1e-4），以避免无效$\log$运算。

除噪声标签问题外，类别不均衡（class imbalance）也是分类任务经常要面对的问题。例如，目标检测任务中可能存在大量”背景物体”，存在正样本标注框远少于负样本标注框的现象，同时不同类之间的分类难度也存在一定差异，这些都会给模型训练带来一定困难。这就需要损失函数可以自动有差别的对待不同类别的预测结果，可以根据预测置信度（因为损失函数的输入只有这一种信息）自动的调整高置信度或者低置信度类别的权重。

焦点损失（focal loss）函数就是一种可自动均衡不同类别权重的损失函数，其定义如下：

(2.3.6)¶\[\mathcal{L}_{\text{focal}}(f({x}),y)=-(1-{p}_y)^\gamma \log({p}_y), \;\; \gamma\geq 0,\]

其中，$\gamma$是调制因子。当$\gamma=0$时，焦点损失退化为交叉熵损失；当$\gamma>0$时，系数项$(1-{p}_y)^\gamma$会对样本进行动态权重调整：当${p}_y$越接近1时，此时模型预测准确，认为样本是容易样本，权重系数变小；当${p}_y$越接近0时，此时模型预测不准确，认为样本是困难样本，权重系数变大。焦点损失最初在目标检测任务中提出，后被广泛应用于其他计算机视觉和自然语言处理任务中，并在解决长尾分布问题方面有显著的效果。

2.3.2. 单点回归损失¶

这里我们先介绍一般的单点回归损失，然后在下一小节中介绍一类特定任务的回归损失，即目标检测中的边框回归损失。在回归问题中，假定标签集为$Y=\{y_i|i=1,\ldots,n; y_i \in \mathbb{R}\}$，样本集合为$X=\{{x}_i|i=1,\ldots,n\}$，假设模型为深度神经网络$f$，问题类型为单点回归问题，即模型输出$f({x})$为输出空间中的单个点（可以是一个标量或多维向量），而不是多个点组成的集合形状（如边框）。基于此设定，下面介绍几个通用的回归损失函数，包括均方误差、平均绝对误差和平滑平均绝对误差。

均方误差（mean squared error, MSE）是回归任务中最常用的损失函数之一，它计算了模型预测值和真实值之间的差值平方和。给定样本${x}$、真实类别$y$、模型$f$，均方差损失定义如下：

(2.3.7)¶\[\label{eq:mse_loss} \mathcal{L}_{\text{MSE}}(f({x}),y) = (y-f({x}))^2.\]

平均绝对误差（mean absolute error，MAE）是另一种用于回归任务的损失函数，它计算了模型预测值和真实值之间的绝对差值之和。给定样本${x}$、真实类别$y$、模型$f$，平均绝对误差损失定义如下：

(2.3.8)¶\[\mathcal{L}_{\text{MAE}}(f({x}),y) = |y-f({x})|.\]

平滑平均绝对误差（Huber loss）是在MAE基础上的一种平滑改进。一般认为，MSE比MAE对异常值更加敏感，因为当出现异常值时，MSE中的平方操作会将其误差加倍放大，会使模型朝异常值拟合的方向优化，影响模型的整体性能。而MAE的问题在于梯度始终一致，即使损失值很小，梯度也会比较大，因而往往需要使用动态学习率的方式帮助MAE更好的收敛。Huber损失结合了MSE和MAE的特点重新设计了损失函数，给定样本${x}$、真实类别$y$、模型$f$，Huber损失的定义如下：

(2.3.9)¶\[\begin{split}\begin{aligned} \mathcal{L}_{\text{huber}}(f({x}),y)=\left\{ \begin{aligned} & \frac{1}{2}(f({x})-y)^2 & |f({x})-y|<\delta \\ & \delta|f({x})-y| - \frac{1}{2} \delta^2 & \text{otherwise}, \end{aligned} \right. \end{aligned}\end{split}\]

其中，$\delta$是超参数，用于调节MAE的平滑程度。可以发现在真实值的近端，Huber损失使用MSE的形式使梯度随优化的进行逐步减小，利于模型最后阶段的参数收尾调优；而在优化目标的远端，Huber损失使用MAE的形式，降低损失函数对于异常点的敏感程度。当$\delta$趋于无穷时，该损失函数将退化为MSE；若$\delta$趋于0，该损失函数将退化为MAE。

2.3.3. 边框回归损失¶

目标检测任务中要求预测物体边框（bounding box）的位置，并对边界框中的物体做出分类。边框位置预测往往被建模成一个边框回归（bounding box regression，BBR）问题，即对边界框四个顶点位置的坐标进行回归。既然是回归问题，那么边框回归就可以使用章节3.3.2中介绍的回归损失函数如MSE、MAE等来解决。但是边框检测的质量是由预测边框和真实边框之间的交并比（intersection over union，IoU）来衡量的，所以使用基于IoU定义的损失函数一般会更加有效 (Rahman and Wang, 2016, Yu et al., 2016) 。

IoU是一种经典的边界框重合度量化方法，它使用预测边框$B$和真实框$A$之间的重叠面积与两框并集面积之间的比值$IoU=\frac{|A \cap B|}{|A \cup B|}$来反映边框预测的准确程度。IoU损失定义如下：

(2.3.10)¶\[\label{eq:iou_loss} \mathcal{L}_{IoU} = 1 - IoU.\]

IoU损失在两个边框完全不重叠时（训练初期或模型发生很大预测错误时）恒为1，且梯度消失。GIoU（generalized IoU）损失通过引入最小包含面积$A_{c}$来解决此问题 (Rezatofighi et al., 2019) 。最小包含面积是可以将预测和真实框都包含在内的最小封闭矩形。GIoU损失的定义如下：

(2.3.11)¶\[\label{eq:giou_loss} \mathcal{L}_{GIoU} = 1 - IoU + \frac{\left|A_{c}-U\right|}{\left|A_{c}\right|},\]

其中，$U=A \cup B$为两个边框的并集面积。

当预测边框和真实框为包含关系时，GIoU退化为IoU，此时无论边框处于什么位置，GIoU和IoU都无法反映出预测框的好坏。针对此问题，DIoU（distance IoU）通过在IoU的基础上添加两个边框中心点距离来解决 (Zheng et al., 2020) 。DIoU损失的定义如下：

(2.3.12)¶\[\label{eq:diou_loss} \mathcal{L}_{DIoU} = 1 - IoU + \frac{\gamma^{2}(b, b^{gt})}{c^{2}},\]

其中，$b$和$b^{gt}$分别表示预测边框和真实框的中心点位置，$\gamma^{2}(b, b^{gt})$表示两个中心点之间的欧氏距离，$c$表示最小包含矩形的对角线距离。

CIoU（complete IoU）损失在DIoU损失的基础上，进一步考虑边框宽高比的尺度信息，设边框的高宽分别为$h$和$w$，真实框的高宽分别为$h_{gt}$和$w_{gt}$，CIoU通过引入长宽的比例信息来精细化的反映预测边框和真实框之间的形状差异。CIoU损失定义如下：

(2.3.13)¶\[\label{eq:ciou_loss} \mathcal{L}_{CIoU} = 1 - IoU + \frac{\gamma^{2}(b, b^{gt})}{c^{2}} + \beta\cdot \frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2},\]

其中，$\beta$ 为权重系数。

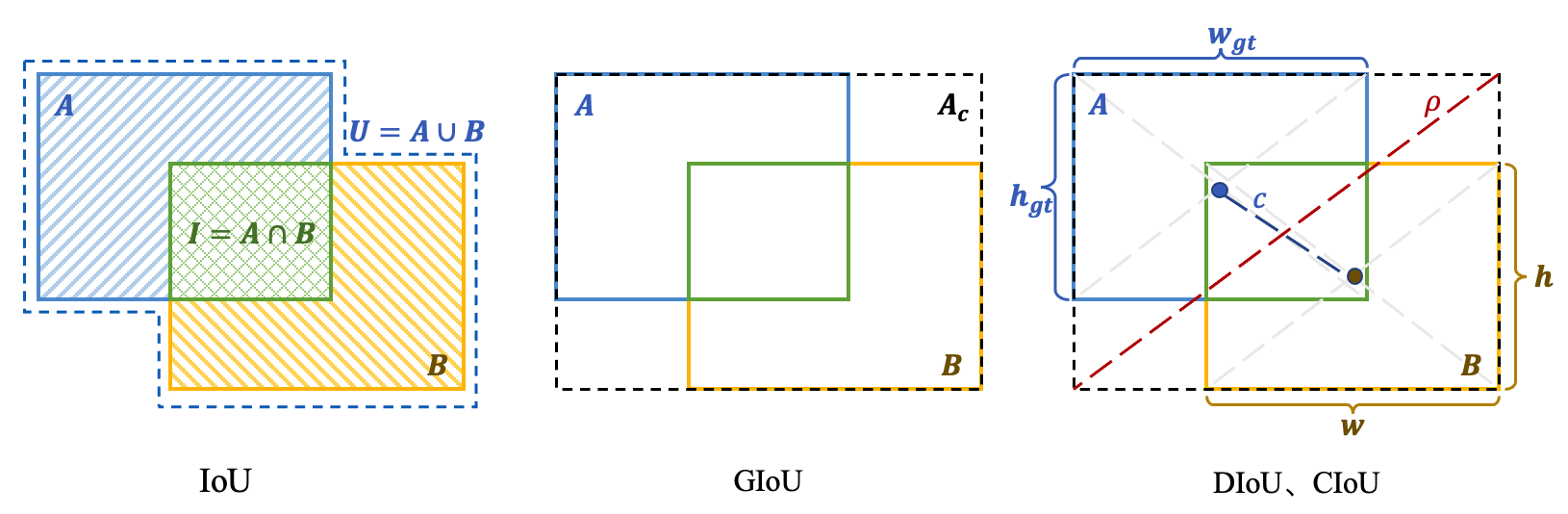
图2.3.1 不同 IoU 变体示意图¶

图2.3.1 综合展示了上述几种IoU变体的不同思想。在此基础上，可以通过向这些损失的IoU项和约束项添加幂变换（power transform）的形式来进一步提高这些损失函数的性能和对噪声边框的鲁棒性。幂变换得到的损失称为$\alpha$-IoU (He et al., 2021) ，上述几种IoU损失的幂形式统一定义如下：

(2.3.14)¶\[\begin{split}\begin{aligned} \left\{ \begin{aligned} & \mathcal{L}_{\alpha-IoU} = 1 - {IoU}^{\alpha} \\ & \mathcal{L}_{\alpha-GIoU}=1-{IoU}^{\alpha}+{(\frac{\left|A_{c}-U\right|}{\left|A_{c}\right|})}^{\alpha} \\ & \mathcal{L}_{\alpha-DIoU}=1-{IoU}^{\alpha}+\frac{\gamma^{2\alpha}\left(b, b^{gt}\right)}{c^{2\alpha}} \\ & \mathcal{L}_{\alpha-CIoU}=1-{IoU}^{\alpha}+\frac{\gamma^{2\alpha}\left(b, b^{gt}\right)}{c^{2\alpha}}+{(\beta v)}^{\alpha}, \end{aligned} \right. \end{aligned}\end{split}\]

其中，$\alpha$为幂变换系数，当$\alpha=1$时$\alpha$-IoU系列损失退化为原损失。$\alpha$-IoU损失可以显著地超过原有损失，对小数据集和噪声的鲁棒性更强，即使在高质量的干净数据上，$\alpha$-IoU损失也能够带来一定的性能提升。

2.3.4. 人脸识别损失¶

人脸识别是多种任务的统称，一般包括两类常见任务：1）人脸验证（face verification），其判断两张人脸图片是否是同一个人；2）人脸鉴别（face identification），其判断人脸照片属于哪一个人。人脸识别一般包括多个步骤：人脸检测（检测人脸在图像中的位置）、关键点定位（定位人脸的关键点）、特征提取（提取人脸特征）、匹配或检索（根据任务执行匹配或检索）。其中，关键点定位和特征提取可以由人脸识别模型的特征提取器部分一步完成，即给定检测出的人脸区域模型直接输出一个人脸特征向量。人脸识别模型往往通过度量学习（或特征学习）的方式来获得强大的特征抽取能力。下面将介绍训练人脸识别模型所使用的损失函数。

假设人脸图片为${x}$，模型提取到的人脸特征为${z}=f({x}) \in \mathbb{R}^d$ 2 ，该图像对应的身份类别为$y$，该类别对应的分类器权重分向量为${W}_y \in \mathbb{R}^d$，身份类别总数为$K$，同时令符号$d(\cdot,\cdot)$表示距离度量函数。下面先介绍人脸识别任务的损失函数。

Softmax损失（也称归一化指数损失）是经典的人脸识别损失函数，它将任务建模为人脸分类问题，即同一个人的人脸图片都被视为同一类，通过有监督学习使模型将不同类别（人的身份）的图片区分开来，从而让模型学到良好的人脸表征提取能力。Softmax损失定义如下：

(2.3.15)¶\[\mathcal{L}_{\text{softmax}}(f({x}),y) = - \log \frac{e^{{W}_y^{\top} {z}}}{\sum_{k=1}^{K} e^{{W}_k^{\top} {z}}},\]

其中，${W}_y$和${W}_k$分别表示类别$y$和$k$所对应的权重分向量。最小化上述损失意味着使人脸特征${z}$与其对应的权重向量${W}_y$内积尽可能小，同时拉大其他类别的权重向量与${z}$的内积，从而达到同一身份的人脸特征互相靠近、不同身份的人脸特征互相拉远的效果。Softmax损失实际上就是在模型$f$+分类头的基础上定义的交叉熵损失，只不过每个人对应一个类别。训练得到的模型$f$便可作为一个高性能特征抽取器，在推理过程中提取人脸特征进行比对，完成相似关系验证证和人脸识别。

Triplet损失（也称三元组损失）:cite:schultz2003learning,schroff2015facenet 与Softmax损失不同，其更关注表征模型输出的相对距离而非绝对距离，是一种经典的度量学习损失函数。在使用Triplet损失时，首先需要构造三元组（Anchor，Positive，Negative），由锚（Anchor）样本、正（Positive）样本和负（Negative）样本组成。其中，以Anchor样本为参照，Positive与Anchor为同一身份的两张不同人脸图片，组成正样本对，对应的特征分别记作${z}_A$和${z}_P$，而Negative与Anchor是不同身份的两张人脸图片，组成负样本对，其对应的特征记作${z}_N$。Triplet损失定义如下：

(2.3.16)¶\[\mathcal{L}_{\text{triplet}}\big({z}_A, {z}_P, {z}_N) = \max(d({z}_A,{z}_P)-d({z}_A,{z}_N)+\gamma, 0 \big),\]

其中，$\gamma$是边界超参，定义了正样本距离和负样本距离之间的最小差距。值得注意的是，在应用Triplet损失之前一般会将人脸特征进行归一化，因而优化距离等价于优化特征之间的角度。相比Softmax损失，通过Triplet损失不需要对每个身份分配一个分类器权重，资源占用较少，但是挑选Anchor、Negative和Positive的方式对其性能影响很大，训练过程容易不稳定，因此在某些场景中人们会将Triplet损失作为一个辅助项。

中心损失（center loss） (Wen et al., 2016) 是对Softmax损失的改进，其通过创建类别特征中心并将同类特征往中心聚拢的方式来提升特征学习效果，从而可以使分类器权重更加接近实际的人脸特征中心。中心损失定义如下：

(2.3.17)¶\[\mathcal{L}_{\text{center}}(f({x}), y) = - \log \frac{e^{{W}_{y}^{\top} {z}+b_{y}}}{\sum_{k=1}^{K} e^{{W}_{k}^{\top} {z}+ b_k}} + \frac{\lambda}{2} \parallel{{z}- {c}_{y}}\parallel^2_2,\]

其中，${W}_y$和${W}_k$分别表示类别$y$和$k$所对应的权重分向量，$b_y$和$b_k$分别表示类别$y$和$k$所对应的偏置，${c}_{y}$表示类别$y$的特征中心向量，可以计算为此类样本的特征均值。考虑到效率问题，人们通常会在每个批中统计并更新各个类别的特征中心${c}_{y}$，特征中心随着模型训练的进行会越来越准确。

大间隔Softmax损失（large-margin softmax loss，L-Softmax） (Liu et al., 2016) 将Softmax中的点积运算拆解为两向量的长度与它们夹角余弦的积 ${W}_{y}^{top} {z}= norm{{bm{W}}\_y}norm{{bm{z}}}cos(theta)[），进而在训练过程中对于正确配对的权重向量和人脸特征的夹角进行扩大（增加:math:\${z}$属于第$i$类而不属于第$j$类，那么这样的方式能够更加严格地约束不等关系：

(2.3.18)¶\[\parallel{{W}_i} \parallel{{z}} \cos(\theta_i) \leq \parallel{{W}_i} \parallel{{z}} \cos(m\theta_i) \leq \parallel{{W}_j} \parallel{{z}} \cos(\theta_j).\]

这种约束也使第$i$类和第$j$类之间产生更宽的分类决策边界。具体地，大间隔Softmax损失定义如下：

(2.3.19)¶\[\label{eq:l-softmax} \mathcal{L}_{\text{L-Softmax}}(f({x}),y) = - \log \frac{e^{\parallel{{W}_y}\parallel{{z}}\phi(\theta_{y,i})}}{e^{\parallel{{W}_y}\parallel{{z}}\phi(\theta_{y,i})} + \sum_{j\neq y} e^{\parallel{{W}_j}\parallel{{z}} \cos(\theta_{j,i})}}\]

(2.3.20)¶\[\begin{split}\begin{aligned} \label{eq:multiplicative-margin} \phi(\theta)=\left\{ \begin{aligned} & \cos(m\theta) & 0\leq \theta \leq \pi/m \\ & {\mathcal{D}}(\theta) & \pi/m < \theta \leq \pi, \end{aligned} \right. \end{aligned}\end{split}\]

其中，${\mathcal{D}}(\theta)$设计为单调递减函数，$\theta_{j,i}$表示权重向量${W}_j$和特征${z}$之间的夹角，函数$\phi$在$\pi/m$处应连续。显然，增大$m$值会增加训练难度，对于特征的区分度提出更高要求，该超参的合理设置会使得类内更为紧凑以及类间更为可分。

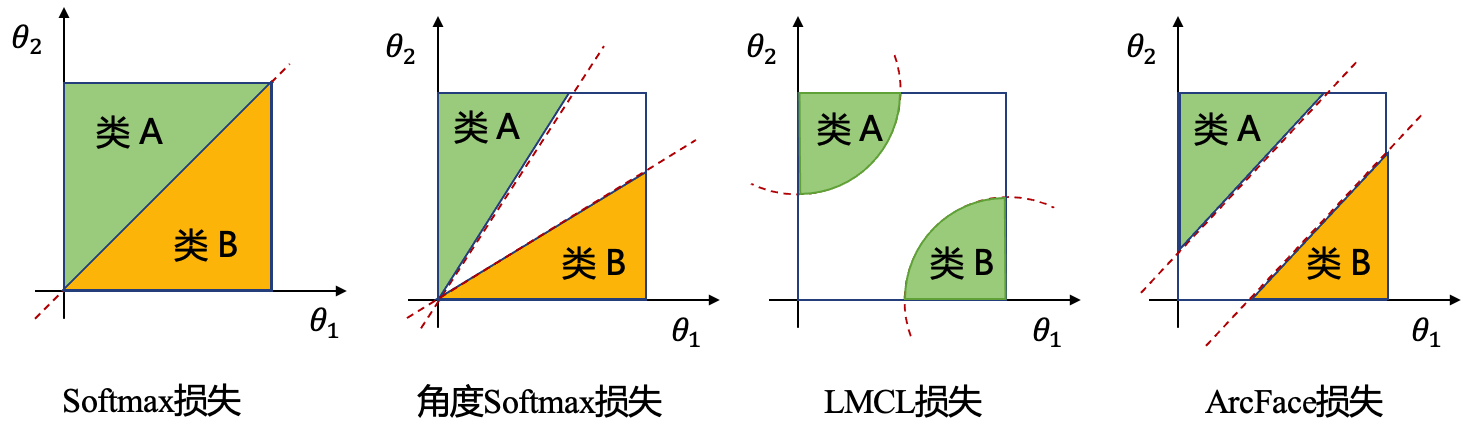
角度Softmax损失（angular softmax loss，A-Softmax） (Liu et al., 2017) 是在大间隔Softmax损失基础上的一个巧妙转化，通过权值归一化使 $\|{{W}}\|=1$ ，从而将权值项从公式 [eq:l-softmax] 移除，得到下列的角度Softmax损失：

(2.3.21)¶\[\label{eq:a-softmax} \mathcal{L}_{\text{A-Softmax}}(f({x}),y) = - \log \frac{e^{\parallel{{z}}\parallel\phi(\theta_{y,i})}}{e^{\parallel{{z}}\parallel\phi(\theta_{y,i})} + \sum_{j\neq y} e^{\parallel{{z}}\parallel \cos(\theta_{j,i})}}.\]

可以看出，角度Softmax损失将特征点映射到单位超球面上，让不同类别的特征只在角度上分离开来，增加角度边界间隔。角度Softmax损失也是SphereFace算法所使用的损失，故也常被称为SphereFace损失。

大间隔余弦损失（large margin cosine loss，LMCL） (Wang et al., 2018) 在角度Softmax损失的基础上提出更近一步归一化特征，并引入两个超参（角度间隔 :math:`{=latex}gamma\和规范化尺度$s$）来调整整体的值域范围。LMCL损失也是训练CosFace算法所使用的损失，故也被称为CosFace损失，具体定义如下：

(2.3.22)¶\[\label{eq:lmcl} \mathcal{L}_{\text{LMCL}}(f({x}),y) = - \log \frac{e^{s\cdot(\cos(\theta_{y,i})-\gamma)}}{e^{s\cdot(\cos(\theta_{y,i})-\gamma)} + \sum_{j\neq y} e^{s \cdot \cos(\theta_{j,i})}}.\]

通过权重归一化和特征归一化，大间隔余弦损失彻底完成了从权重和特征空间到单纯余弦空间的转换，避免了不同类别之间由于特征不均衡导致的间隔差异。

加性角度间隔损失（ArcFace loss） (Deng et al., 2019) 的思想和LMCL损失类似，区别是将角度间隔超参 :math:`{=latex}gamma\直接加在了余弦函数内的角度上（LMCL是加在了余弦函数值上）。一般来说，角度距离比余弦距离对角度的影响更加直接，所添加的角度等同于超球面的测地距离。ArcFace损失的定义如下：

(2.3.23)¶\[\label{eq:arc_face} \mathcal{L}_{\text{ArcFace}}(f({x}),y) = - \log \frac{e^{s\cdot(\cos(\theta_{y,i} + \gamma))}}{e^{s\cdot(\cos(\theta_{y,i} + \gamma)-\gamma)} + \sum_{j\neq y} e^{s \cdot \cos(\theta_{j,i})}}.\]

不同人脸识别损失的决策边界示意图 :label:fig:face_losses

:numref:fig:face_losses 展示了前面介绍的几种边界损失的决策边界，从角度Softmax损失的乘法角度间隔（公式[eq:a-softmax]和[eq:multiplicative-margin]），到LMCL损失的加法余弦间隔（公式[eq:lmcl]），再到ArcFace损失的加性角度间隔（公式[eq:arc_face]）。这些损失通过变换边界间隔的形式不断提高对特征的约束，此外还可以与其他度量学习损失如Triplet损失和中心损失等进行结合，进一步提升特征学习能力。

2.3.5. 自监督学习损失¶

自监督学习的核心是表征学习（representation learning）（也称特征学习），即从大规模无标注数据中学习数据本质的特征，从而获得一个强大的特征抽取器。自监督表征学习在深度学习中有着重要的用途，即大规模预训练。对比学习和重构学习是两类重要的自监督学习手段。对比学习的主要思想是让相似的样本离的更近，不相似的样本离的更远。模型在对比学习过程中逐渐掌握数据内在的规律，将样本聚成几个特征的簇，进而通过增加簇内和簇间特征约束，即“簇内更汇聚、簇间更分散”，鼓励模型学习到样本更本质的特征。重构学习的主要思想是通过“破坏-恢复”的方式让模型学习数据深层的特征，“破坏”的方式包括数据增广、随机删除等。下面介绍这两类学习方法所使用的损失函数。

InfoNCE损失（Info noise contrastive estimation loss） (Oord et al., 2018) 是自监督预训练中最常用的一种对比学习损失。对比学习的核心在于让模型学习到相同数据在不同视角下的一致性表征，让同一样本的不同数据增广版本组成正样本对、不同样本组成负样本对，再通过对比学习拉近正样本间的距离、拉远负样本间的距离，让模型学习到数据的一致性。InfoNCE损失的定义如下：

(2.3.24)¶\[\mathcal{L}_{\text{InfoNCE}}({z}_A, {z}_P, Z_N) = -\log \frac{\exp({z}_A\cdot {z}_P/\tau)}{\sum_{{z}_i \in Z_N} \exp({z}_A \cdot {z}_i/\tau)},\]

其中，${z}_A$为锚（anchor）样本的逻辑值（logits），${z}_P$为正样本的逻辑值（一个锚样本对应一个正样本），$Z_N=\{{z}_i\}_{i=1}^{K}$为$K$个负样本的逻辑值组成的集合（一个锚样本对应$K$个负样本），$\tau$是超参温度系数。锚样本和正样本可以是同一个样本的两个不同增广版本，即对同一个样本独立使用两次数据增广得到的两个增广后的样本。值得一提的是，InfoNCE还有其他版本的定义，如自监督学习方法MoCo（momentum contrast）里的基于查询（query）和键值（key）的定义 (He et al., 2020) 。我们这里采用的是Triplet风格的定义。

均方误差（MSE）是基于重构的自监督学习最经常使用的损失函数。与对比学习不同，基于重构的自监督学习利用掩码抹除输入数据的部分信息，通过让模型学习重构原始数据的过程来实现模型的自我监督训练。不同的重建任务一般要求模型具有不同的解码器，例如在视觉任务方面，解码器要进行像素重建；而在自然语言处理任务方面，解码器预测遗失的词。重构也可以被看作是一种生成任务，所使用的损失函数会涉及到上文讲述的回归损失函数和分类损失函数，如在掩码自编码器（masked autoencoders，MAE）方法 (He et al., 2022) 中，作者设计了基于均方误差的损失函数衡量模型重构图片的质量。均方误差我们在回归损失中已经介绍，这里不再赘述，但值得注意的是，MAE中的MSE损失只在掩掉的补丁上定义。

2.4. 优化方法¶

前一小节介绍了几种常见任务所使用的损失函数，优化方法的目标就是通过最小化这些损失函数定义的经验损失来更新模型的参数，从而寻找到具有最优泛化性能的模型参数。根据优化方法在优化过程中所使用的梯度信息，现有优化方法可大体分为：一阶优化算法、二阶优化算法和零阶优化算法（又称黑盒优化算法）。其中，一阶优化算法使用一阶梯度信息制定更新策略对模型参数进行更新，需要模型是可导的；二阶优化算法需要二阶梯度信息（精确的或估计的）来确定梯度下降最快的方向；而零阶优化算法无法计算梯度信息，只能以探索、进化的方式来估计梯度信息。这三类优化方法不只用于正常训练一个机器学习模型，还被攻击者和防御者用来设计新的攻击和防御方法，展开人工智能安全攻防。考虑到计算效率和应用场景等问题，目前深度学习领域主要使用的是一阶优化算法，因此本小节选择介绍几个经典的一阶梯度优化算法。有些攻击研究（如黑盒对抗攻击）所使用的零阶优化方法会在后续章节中结合具体的攻击方法单独进行介绍。

2.4.1. 梯度下降¶

下面我们以有监督学习任务为例来介绍梯度下降（gradient descent）。给定一个有监督学习任务和训练数据集$D=\{({x}_i,y_i)\}_{i=1}^{n}$、模型$f_{\theta}$（$\theta$为模型参数）、损失函数$\mathcal{L}$，优化的目标是寻找一组最优参数$\theta^{*}$可以最小化模型$f$在训练数据集$D$上的经验错误$J(\theta)$。其中，经验错误是模型在所有训练样本上的平均损失，由损失函数$\mathcal{L}$定义如下：

(2.4.1)¶\[\label{eq:objective_function} J(\theta) = \frac{1}{n}\sum_{i=1}^{n} \mathcal{L}(f({x}_i), y_i).\]

$J(\theta)$是我们优化的目标函数，它是一个关于优化变量$\theta$的函数。如果$J(\theta)$的形式非常简单，比如是显示定义的或者单调的，那么就可以通过直接求解的方式寻找其极值点和对应的最优解$\theta^{*}$；如果$J(\theta)$形式未知但是是一个严格凸函数（strictly convex function），则可以通过一阶或二阶导数信息找到最优解。然而，复杂的深度神经网络所表示的函数往往是高度非线性的，导数为零的解析式往往难以求解，而如果使用基于搜索的方式寻找最值，当优化对象$\theta$维度增大时，在高维参数空间中进行搜索无论从精度还是效率都变得难以接受。

梯度下降法以一组随机参数$\theta^{0}$为出发点，沿着一阶导数$\nabla_{\theta}J(\theta)$的反方向，逐步逼近目标函数$J(\theta)$的最小值。梯度下降的过程可形式化表示如下：

(2.4.2)¶\[\begin{split}\begin{aligned} \label{eq:gd} \begin{aligned} \theta^{t+1} & = \theta^{t} - \eta\nabla_{\theta}J(\theta^{t}) \\ & = \theta^{t} - \eta\frac{1}{n}\nabla_{\theta} \sum_{i=1}^{n} \mathcal{L}(f({x}_i), y_i), \end{aligned} \end{aligned}\end{split}\]

其中，$\eta$为学习率（即梯度下降的步长），$t+1$为当前步数，也是模型参数更新的次数。可以看出，梯度下降是定义在所有$n$个训练样本上的，即需要在全部$n$个样本上计算一遍梯度后才能更新一次模型参数。此外，模型的参数$\theta$是一个$m$维的高维向量，即$\theta=[\theta_1, \theta_2, \cdots, \theta_m]^{\top}$，所以导数$\nabla_{\theta}J(\theta)$对应下面的偏导数向量：

(2.4.3)¶\[\label{eq:partial_gradients} {g}= [\frac{\partial J(\theta)}{\partial \theta_1}, \frac{\partial J(\theta)}{\partial \theta_2}, \cdots, \frac{\partial J(\theta)}{\partial \theta_m}]^{\top}.\]

学习率（步长）在梯度下降中起到至关重要的作用。一般地，只要步长$\eta$足够小且不陷入局部最优，那么梯度下降总能找到一组全局最优的参数$\theta^{*}$使模型的经验错误$J(\theta)$取得最小值。对深度神经网络来说，目标函数$J(\theta)$是非凸的，往往存在很多局部最优解，这就需要调整学习率来避免陷入局部最优解。学习率的调整除了可以帮助跳出局部最优解以外，还会直接影响收敛速率：过小的学习率会导致参数更新过慢，大大增加训练时间；而过大的学习率则会破坏梯度的局部代表性，导致训练不稳定，模型无法收敛到最优。

2.4.2. 随机梯度下降¶

如公式[eq:gd]所定义的，梯度下降算法的每一次迭代更新的计算复杂度为$O(n)$（即在所有$n$个样本上计算梯度），与训练数据的规模呈线性增长的关系。这种线性增长关系使得当数据集的规模非常大时，每一步参数的迭代更新将消耗非常长的时间，这时候基于梯度下降的优化策略已经不适用。为了适应这一情况，随机梯度下降（stochastic gradient decent，SGD）算法被提出。梯度$\nabla_{\theta}J(\theta^{t})$的计算是梯度下降算法中最核心、最耗时的部分，其可重表示如下：

(2.4.4)¶\[\label{eq:exp_nabla} \nabla_{\theta}J(\theta^{t}) = \nabla_{\theta} \mathbb{E}_{({x},y) \in D} \mathcal{L}(f({x}),y) = \mathbb{E}_{({x},y) \in D} \nabla_{\theta} \mathcal{L}(f({x}),y).\]

通过上式可以看出，期望损失的梯度可以等价于梯度的期望，而期望的计算可以通过采样进行近似。随机梯度下降的主要思想就是用更小规模的样本来近似损失梯度的期望，从而降低梯度下降中每一次梯度计算的复杂度。具体来说，在每一次更新迭代的过程中，随机从$n$个样本中采样出一小批（minibatch）的样本，记为$X_B$（$n_B=|X_B| \ll n$），并使用下面的公式迭代更新模型参数：

(2.4.5)¶\[\label{eq:sgd} \theta^{t+1} = \theta^{t} - \eta \frac{1}{n_B}\sum_{i=1}^{n_B} \nabla_{\theta} \mathcal{L}(f({x}_i), y_i).\]

上式便是随机梯度下降（SGD）的参数更新策略。在实际任务中，我们往往采用基于小批量（minibatch）的随机梯度下降，也称小批量随机梯度下降，即$n_B > 1$（$n_B$根据训练需求一般设置为几百或几千）。

2.4.3. 改进的随机梯度下降¶

尽管SGD方法提升了优化效率，但是它并不能保证优化方法一定具有很好的收敛性，其优化过程还存在一些挑战。首先，初始学习率对于优化结果非常重要，但是选择最优的初始学习率存在一定的挑战。其次，随着训练的进行和模型的收敛，学习率往往需要做适当的调整，这给SGD的固定学习率策略带来挑战。虽然有一些学习率的调节器如线性调节器和余弦调节器可以使用，但是在一个周期内学习率也是固定的。固定学习率会给SGD带来：学习过程有时候会很慢、每次更新可能会不按照正确的方向进行、参数更新往往存在高方差的现象、目标函数在优化过程中发生剧烈抖动等问题。此外，高度非凸优化的关键在于如何避免局部最优解和鞍点（saddle points）。鞍点通常位于一个平坦的区域，区域内的所有的点都具有相似的误差且梯度为零，很容易困住小步长的随机梯度下降。为了解决上述问题，一系列基于SGD的改进优化算法被提出，以下将简单介绍几种常见的改进算法。

动量SGD（SGD with momentum） (Qian, 1999) ，其将动量的概念引入SGD来帮助逃逸鞍点并加速SGD的收敛。动量法利用历史梯度信息完成对参数更新的动量累积，通过比较历史梯度与当前梯度，同向加速、反向减速。具体来说，动量SGD将历史梯度信息与当前梯度信息进行加权求和得到当前参数的更新大小，定义如下：

(2.4.6)¶\[\begin{split}\begin{aligned} \label{eq:sgdwithmomentum} \begin{aligned} & v^{t} = \gamma v^{t-1} + \eta \nabla_{\theta} J(\theta^{t}) \\ & \theta^{t+1} = \theta^t - v^t, \end{aligned} \end{aligned}\end{split}\]

其中，$\gamma$为动量参数，$\eta$为学习率，$\theta^t$为第$t$步迭代对应的模型参数。可以看到，动量SGD计算了历史梯度的指数衰减移动平均值，使得实际更新梯度既包含之前梯度的信息又有当前梯度的信息。在原始的SGD中，步长取决于某一时刻的梯度和学习率，而在动量SGD方法中，步长取决于梯度序列的大小和排列。在实际中，动量参数$\gamma$的取值一般为0.5、0.9或0.99，有时也会让$\gamma$随时间不断调整，例如以较小初始值开始，随后逐渐增大，逐步提高历史梯度的重要性。动量法在处理带噪声的梯度情况中具有一定优势。

Nesterov加速的SGD（SGD with Nesterov acceleration） (Nesterov, 1983) 是动量SGD算法的另一变种。我们可以使用与动量SGD相同的符号来描述Nesterov加速的SGD的更新方式如下：

(2.4.7)¶\[\begin{split}\begin{aligned} \label{eq:sgdwithnacc} \begin{aligned} & v^{t} = \gamma v^{t-1} + \eta \nabla_{\theta} J(\theta^{t}-\gamma v^{t-1}) \\ & \theta^{t+1} = \theta^{t} - v^{t}. \end{aligned} \end{aligned}\end{split}\]

可以看出该方法使用了与动量SGD非常类似的指数衰减移动平均策略累积梯度序列，最大的不同点在于该方法并不使用当前梯度，而是根据累计梯度对参数进行一次临时更新，即$\theta^{t}-\gamma v^{t-1}$，在临时更新后再计算梯度并将其与历史梯度进行加权求和，并最终更新模型参数。

AdaGrad (Duchi et al., 2011) 是经典的自适应学习率优化算法，能够自适应调整每个参数的学习率。在优化过程中，AdaGrad需要累计所有历史梯度的平方总和，用于缩放每一个参数的更新步长。AdaGrad的参数更新公式如下：

(2.4.8)¶\[\begin{split}\begin{aligned} \label{eq:adagrad} \begin{aligned} \theta^{t+1} & = \theta^{t} - \frac{\eta}{\sqrt{ G^t + \epsilon}} \cdot {g}^{t} \\ G^t & = G^{t-1} + ({g}^t)^2 = \sum_{t} ({g}^t)^2, \end{aligned} \end{aligned}\end{split}\]

其中，$\theta^{t}$表示$t$时刻模型第$i$维的参数$\theta$，${g}^t$表示$t$时刻$\theta$的梯度（基于小批量计算得到的梯度），$G^t$是过去$t$个时刻的累积梯度平方和，$\epsilon$是为了维持数值稳定性而添加的一个常数，如$10^{-5}$。 AdaGrad可以针对每个参数自适应调整其学习率，对于出现频率较低的特征对应的参数，将采用更大的更新步长，对于出现频率较高的特征对应的参数，将采用较小的更新步长。然而，对于训练深度神经网络模型而言，AdaGrad方法从训练开始就累计梯度平方会导致学习率过早或过量地减少，即学习率容易很快降到接近零。

RMSProp优化算法 (Tieleman et al., 2012) 对AdaGrad中累计历史梯度平方的操作进行了改进，将累计方式更改为指数加权移动平均，通过指数衰减平均能够更好地降低“遥远”的历史梯度信息的影响，从而解决了AdaGrad学习率极速衰减问题。RMSProp的参数更新公式如下：

(2.4.9)¶\[\begin{split}\begin{aligned} \label{eq:RMSProp} \begin{aligned} \theta^{t+1} & = \theta^{t} - \frac{\eta}{\sqrt{ G^t + \epsilon}} \cdot {g}^{t} \\ G^t & = \gamma G^{t-1} + (1-\gamma) ({g}^t)^2, \end{aligned} \end{aligned}\end{split}\]

其中，$\gamma$是衰减系数。对比公式[eq:adagrad]和公式[eq:RMSProp]可以看出，RMSProp与AdaGrad的唯一不同是累积梯度的方式多了一个衰减系数$\gamma$。

AdaDelta (Zeiler, 2012) 与RMSProp的思想非常类似，同样引入了历史梯度的指数加权平方和作为学习率的自适应缩放系数，二者的主要区别在于AdaDelta进一步将学习率 :math:`{=latex}eta\替换为自变量历史变化平方的指数移动平均，避免了手动设置学习率。AdaDelta的参数更新公式如下：

(2.4.10)¶\[\begin{split}\begin{aligned} \label{eq:AdaDelta} \begin{aligned} \theta^{t+1} & = \theta^{t} - \frac{\sqrt{ \Delta \theta^{t} + \epsilon}}{\sqrt{ G^t + \epsilon}} \cdot {g}^{t} \\ G^t & = \gamma G^{t-1} + (1-\gamma) ({g}^t)^2\\ \Delta \theta^{t} & = \gamma \Delta \theta^{t-1} + (1-\gamma) (\theta^{t} - \theta^{t-1})^2, \end{aligned} \end{aligned}\end{split}\]

其中，$\gamma$是衰减系数，$\Delta \theta^{t}$是参数$\theta$过去$t$个时刻自变量历史变化平方的指数移动平均。

Adam (Kingma and Ba, 2015) 是另一种学习率自适应算法，是动量SGD和RMSProp的一种融合。在Adam中，动量并入了梯度一阶矩的估计，并且包括了偏置修正，修正从原点初始化的一阶矩和二阶矩的估计，估计和偏置修正分别对应公式 [eq:adamappro]和公式 [eq:adamapadj]。Adam的参数更新公式如下：

(2.4.11)¶\[\begin{aligned} \theta^{t+1} = \theta^t - \frac{\eta}{\sqrt{\hat{v}^t} + \epsilon} \hat{m}^t \end{aligned}\]

(2.4.12)¶\[\begin{split}\begin{aligned} \label{eq:adamappro} \begin{aligned} m^t = \gamma_1 m^{t-1} + (1-\gamma_1){g}^t \\ v^t = \gamma_2 v^{t-1} + (1-\gamma_2)({g}^t)^2 \end{aligned} \end{aligned}\end{split}\]

(2.4.13)¶\[\label{eq:adamapadj} \begin{aligned} \hat{m}^t = \frac{m^t}{1-\gamma_1^t}, \;\; \hat{v}^t = \frac{v^t}{1-\gamma_2^t}. \end{aligned}\]

通过上面的介绍可以看到，在SGD的基础上发展出了许多变体SGD优化算法。其中，很多变体如AdaGrad、RMSProp、AdaDelta、Adam等都使用了历史梯度信息，这些信息包含了梯度的变化趋势，实际上已经相当于使用了二阶梯度信息，所以算是介于一阶和二阶之间的优化算法。很多SGD的变体在一些问题上可以带来显著的收敛速率提升，但是最终得到的解很多时候并不比SGD更优，所以在具体的实际应用中应该哪种优化算法领域内没有达成共识。

2.5. 本章小结¶

本章主要从机器学习的基本概念、学习范式、损失函数、以及优化方法四个方面对机器学习基础知识进行了较为全面的介绍。机器学习的基本流程并不复杂，根据实际问题定义学习任务，收集训练数据，定义损失函数，选择合适的模型和优化器并进行训练，即可得到一个机器学习模型用于部署。复杂的是整个过程中所面临的一些现实挑战，比如无法收集到某一类型的样本、计算资源受限、模型泛化性能无法估计等等。在这种背景下，我们在实践中的每一种妥协性假设、每一个替代性选择就会带来额外的安全风险，比如借助网上的开放数据或者第三方预训练模型就难免会带来被后门和投毒攻击的风险。本章介绍的机器学习基础知识将有助于后续章节中人工智能安全问题与方法的理解。

1: 本书会在无严重歧义的情况下复用一些符号，如$A$在章节3.2.2中也被用来表示算法。
2: 这里，模型$f$为特征抽取器，输出为人脸特征。